Sunday, October 30, 2022

Wednesday, October 26, 2022

Tuesday, October 25, 2022

Pengertian Dan Fungsi Corong Pemisah (Separator Funnel)

Pengertian Dan Fungsi Corong Pemisah (Separator Funnel)

Pengertian Dan Fungsi Corong Pemisah (Separator Funnel): Corong pisah adalah peralatan laboratorium yang terbuat dari gelas yang biasanya digunakan untuk proses pemisahan cairan dari dua fase yang tidak dapat bercampur. Corong pemisah ini berbentuk kerucut yang ditutupi setengah bola. Dan alat ini mempunyai penyumbat di atasnya dan keran di bawahnya. Tersedia berbagai ukuran corong pemisah diantaranya adalah : 250 ml, 500 ml, dan 1000 ml.

Tuesday, October 4, 2022

Sunday, November 22, 2020

 An Evaluation of Backpropagation Interpretability for Graph Classification with Deep Learning

 

A summary of the IEEE BigData 2020 research paper by Kenneth Teo Tian Shun, Eko Edita Limanta, and Arijit Khan

 

[Graph Classification] Graph data are ubiquitous in many domains, such as social networks, knowledge graphs, biological networks, geo-spatial road networks, and internet-of-things. There are plenty of interest and applications in developing high-quality machine learning techniques for classifying graph objects, including cheminformatics (e.g., compounds that are active or inactive for some target) [1], [2] and bioinformatics (e.g., classifying proteins into different families) [3], malware detection and classification with call graphs [18]. There are two research directions for classification tasks on graphs: (1) Given a single large graph, infer labels of individual nodes (the node classification problem) [4], [5]; and (2) given a set of graphs with different structure and sizes, predict the class labels of unseen graphs (the graph classification problem) [6], [7], [19]. We focus on the second problem — graph classification, which is more difficult because graph datasets contain graphs with varying numbers of nodes and edges.

 

[Why Deep Learning in Graph Classification] Unlike images, general graphs do not have regular grid-like structures, and the neighborhood size of each node varies to a great extent. The lack of ordered vector representation limits the applicability of machine learning on graphs, and consequently, makes it difficult to build a classifier directly over the graph space [19], [7]. In the past, graph kernels (e.g., random walks, shortest paths, cyclic patterns, subtrees, graphlets, and subgraph kernels) [8] and feature based classification (e.g., frequent and significant subgraphs) methods [9], [10] were developed. Due to the challenges of feature engineering, coupled with the hardness of subgraph mining and isomorphism testing, deep learning methods are increasingly becoming popular. In particular, the end-to-end nature of learning in convolutional neural networks (CNNs) and their ability to extract localized spatial features, have turned them into powerful tools for learning from a large corpus of data including graphs. We focus on three state-of-the-art graph convolutional neural networks (GCNNs): GCNN with global average pooling (GCNN+GAP)[11], [5], DGCNN [19], and DIFFPOOL [7], as well as their variants.

 

[Interpretability Challenges in Deep Learning-based Graph Classification] Deep learning models and neural networks are “black-box” — it is inherently difficult to understand which aspects of the input data drive the decisions of the network. Interpretability can improve the model’s transparency related to fairness, privacy, and other safety challenges, thus enhancing the trust in decision-critical applications [12], [13]. Network data are complex, noisy, and content-rich. End users (e.g., data scientists, business analysts) often find them difficult to query and explore [14]. Hence, it is even more critical to provide human-understandable interpretation over classification results on such datasets. While interpretability for GCNNs is an open area of research, inspired by recent interpretability tools for CNNs, in this work we investigate three backpropagation based post-hoc interpretability methods: (1) saliency map with contrastive gradients (CG) [15], (2) gradient-weighted class activation mapping (Grad-CAM) [16], and (3) deep learning important features (DeepLIFT) [17]. We conduct a thorough experimental evaluation of these interpretability methods in conjunction with three state-of-the-art graph convolutional neural networks: GCNN+GAP [11], [5], DGCNN [19], and DIFFPOOL [7], and with their variants.

We design novel strategies for integrating them, measuring their efficiency and performance both qualitatively and quantitatively. We implement GCNNs and interpretability tools in a common environment, using same hyperparameters selection criteria, and present extensive empirical comparisons over five real-world graph datasets from different categories. We report their quantitative, visualization, and active subgraph based performance, compare them with the classic significant subgraph mining results [10], summarize their trade-offs, and provide guidelines for researchers and practitioners.

[Summary and our recommendation] The following table summarizes our recommendation levels of each interpretability method according to different performance metrics. The scale is from 1 to 4 stars, larger number of stars stands for higher recommendation. Clearly, there is no single winner.



(1) Considering various trade-offs, our recommended interpretability tools for graph classification are DeepLIFT, GradCAM, in combination with recent (and more accurate) GCNNs: DGCNN, DIFFPOOL, and its variant DIFFPOOL_D. (2) Grad-CAM is useful for class-discriminative visualization, whereas DeepLIFT can identify differences between two individual instances. (3) Finally, DIFFPOOL and DIFFPOOL_D can assist visualizing node clustering at various granularity, and this has the potential to identify active subgraphs, e.g., active functional groups for biological networks classification.

 

We open sourced an end-to-end framework (https://github.com/tsKenneth/interpretable-graph-classification) in which one can plug and play with different graph datasets, GCNNs, and backpropagation-based interpretability tools. In future, it would be interesting to test and model how high accuracy and fidelity could impact the user’s trust in the underlying graph classification tool, as well as to conduct usability analysis due to higher contrastivity, sparsity, explanation subgraph size, and efficiency.


For more information, click here for our paper. Code: GitHub.

 

References

[1] Z. Wu, B. Ramsundar, E. N. Feinberg, J. Gomes, C. Geniesse, A. S. Pappu, K. Leswing, and V. S. Pande, “MoleculeNet: A Benchmark for Molecular Machine Learning”, CoRR, vol. abs/1703.00564, 2017.

[2] D. Duvenaud, D. Maclaurin, J. A.-Iparraguirre, R. G.-Bombarelli, T. Hirzel, A. A.-Guzik, and R. P. Adams, “Convolutional Networks on Graphs for Learning Molecular Fingerprints,” NeurIPS, 2015.

[3] R. Sharan, S. Suthram, R. M. Kelley, T. Kuhn, S. McCuine, P. Uetz, T. Sittler, R. M. Karp, and T. Ideker, “Conserved Patterns of Protein Interaction in Multiple Species”, PNAS, vol. 102, no. 6, 2005.

[4] J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun, “Spectral Networks and Locally Connected Networks on Graphs,” ICLR, 2014.

[5] T. N. Kipf and M. Welling, “Semi-Supervised Classification with Graph Convolutional Networks”, ICLR, 2017.

[6] D. Duvenaud, D. Maclaurin, J. A.-Iparraguirre, R. G.-Bombarelli, T. Hirzel, A. A.-Guzik, and R. P. Adams, “Convolutional Networks on Graphs for Learning Molecular Fingerprints,” NeurIPS, 2015.

[7] Z. Ying, J. You, C. Morris, X. Ren, W. L. Hamilton, and J. Leskovec, “Hierarchical Graph Representation Learning with Differentiable Pooling”, NeurIPS, 2018.

[8] S. V. N. Vishwanathan, N. N. Schraudolph, R. Kondor, and K. M. Borgwardt, “Graph Kernels”, J. Mach. Learn. Res., vol. 11, 2010.

[9] X. Yan, H. Cheng, J. Han, and P. S. Yu, “Mining Significant Graph Patterns by Leap Search”, SIGMOD, 2008.

[10] S. Ranu and A. K. Singh, “GraphSig: A Scalable Approach to Mining Significant Subgraphs in Large Graph Databases”, ICDE, 2009.

[11] M. Lin, Q. Chen, and S. Yan, “Network In Network”, ICLR, 2014.

[12] M. Du, N. Liu, and X. Hu, “Techniques for Interpretable Machine Learning”, Commun. ACM, vol. 63, no. 1, 2020.

[13] Z. C. Lipton, “The Mythos of Model Interpretability”, Commun. ACM, vol. 61, no. 10, 2018.

[14] N. Jayaram, A. Khan, C. Li, X. Yan, and R. Elmasri, “Querying Knowledge Graphs by Example Entity Tuples”, IEEE Trans. Knowl. Data Eng., vol. 27, no. 10, 2015.

[15] K. Simonyan, A. Vedaldi, and A. Zisserman, “Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps”, ICLR, 2013.

[16] R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam, D. Parikh, and D. Batra, “Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization”, ICCV, 2017.

[17] A. Shrikumar, P. Greenside, and A. Kundaje, “Learning Important Features Through Propagating Activation Differences”, ICML, 2017.

[18] M. Fan, X. Luo, J. Liu, M. Wang, C. Nong, Q. Zheng, and T. Liu, “Graph Embedding based Familial Analysis of Android Malware using Unsupervised Learning,” ICSE, 2019.

[19] M. Zhang, Z. Cui, M. Neumann, and Y. Chen, “An End-to-End Deep Learning Architecture for Graph Classification”, AAAI, 2018.

Friday, June 5, 2020

Mining Top-k Pairs of Correlated Subgraphs in a Large Network

Mining Top-k Pairs of Correlated Subgraphs in a Large Network

A summary of the VLDB 2020 research paper by Arneish Prateek, Arijit Khan, Akshit Goyal, and Sayan Ranu

[Background and Problem]  A large body of work exists on mining recurring structural patterns among a group of nodes in the form of frequent subgraphs [1, 2]. However, can we mine recurring patterns among the frequent subgraphs themselves? In this paper, we explored this question by mining correlated pairs of frequent subgraphs. Correlated subgraphs are different from frequent subgraphs due to the flexibility in connections between constituent subgraph instances. To elaborate, in Figure 1, we highlight three regions inside the chemical structure of Taxol, an anti-cancer drug, where CCCH and O occur closely albeit connected in different ways in all three instances. For simplicity, we do not consider the edge types (i.e., single or double bonds) in this example. This figure illustrates that while CCCH and O form a frequently occurring correlated pair of subgraphs, the individual instances (for example, HCC(-O)C) may not be frequent patterns themselves. Therefore, existing frequent subgraphs mining techniques cannot mine such pairs of correlated subgraph patterns.
Figure 1: Correlation between CCCH and O in Taxol, an anticancer drug. CCCH and O frequently occur closely but can be connected in multiple different ways.

[Application Scenarios] Correlated subgraphs mining (CSM) will be useful for many applications. For example, it can be used in the identification of co-operative functions in biological networks. In a genome graph of an individual, a node represents a gene and each edge denotes the interaction between two genes. In practice, there are some combinations of dominant genes that co-occur frequently, and these are more likely to express critical phenotypes of the individual. Previous studies show that some pairs of dominant gene combinations co-occur in each individual, and such co-occurring patterns often reflect the joint functionality that is needed for co-operative biochemical functioning such as chemical bonding and binding sites interactions [18]. Based on pairs of correlated genes, we can predict co-operative biological functions of an individual.

To demonstrate the utility of CSM, we present insights derived from the correlated pairs mined in the following datasets.

Figure 2: (a-d) Correlated subgraph pairs <Q1, Q2> and <Q3, Q4> in Yeast. (e) Correlated pair in LastFM. CP denotes Coldplay and RH denotes Radiohead. (f) Correlated pair in Coauthor. 

Yeast [19]. The node labels (Gene Ontology tags) in this Protein Interaction (PPI) network indicate their biological function. In Figure 2, we present two of the top-10 correlated pairs mined. Figures 2a (Q1) and 2b (Q2) show the first pair. Q1 is constituted entirely of units specialising in ion binding, and Q2 is composed of those specialising in transferase activity. Keike et al. [23, 24] have shown that transferases can gain enzymatic activity following the binding of ionic ligands, undergoing conformational changes to insulate the ligands from surrounding water molecules. We highlight another pair < Q3, Q4> in Figures 2c and 2d. Q3is made up of genes that handle responses to chemicals and Q4 is associated with transcription. This co-occurrence is not a coincidence. Specifically, the Gene Ontology [22] database describes in detail the involvement of positive transcription regulation in cellular response to chemical stimulus. Finally, we verified each of the top-10 correlated pairs through domain experts to determine what percentage of pairs suggested biological correlation. The experts could not reject any pair as biologically non-linked. In their opinion, all 10 correlated pairs are either definitely linked, or suggest interesting correlations requiring further investigation.

LastFM [20]. Figure 2e depicts a correlated pair from the top-k set. This pair showcases that communities of users who like the music band Coldplay, are often in close proximity to communities of users who like Radiohead. These two bands are contemporaries, originate from UK and they are often compared on social media.

Coauthor [21]. Figure 2f presents a pair from the top-10 list in the Coauthor (DBLP) network. Nodes correspond to authors and node labels denote the most frequent publication venue of the authors. In this regard, the presented pair is interesting since it reveals proximity between the networking community (ICCCN) and the architecture community (SIGARCH). While most of the other pairs are between conferences centered on similar areas, this pair shows that there is high collaboration between networking and architecture communities. More importantly, this pair reveals that correlated subgraphs may unearth non-trivial connections between communities.

These case-studies illustrate how our proposed CSM can be useful in solving real-life problems.

[Challenges and Differences with Related Work] 
Frequent subgraphs mining. Detecting correlated subgraphs is harder than the frequent subgraphs mining (FSM) problem [1, 2], which already has an exponential search space (a graph with m edges can have 2msubgraphs). Techniques have also been developed for discriminative [3, 4], statistically significant [5, 6, 7, 8, 9] and representative subgraphs mining [10, 11, 12, 13]. For correlated subgraphs mining (CSM), the search space is doubly exponential (because one needs to compute the correlation between every pair of subgraph instances). Additionally, unlike FSM, CSM neither exhibits downward closure nor upward closure, thereby making it difficult to directly apply apriori-based pruning techniques. Moreover, only mining frequent subgraphs is not sufficient for our problem. Since we call subgraph A as correlated to subgraph B if their instances are frequently located close to each other, we need to enumerate all instances of those frequent subgraphs for computing the degree of correlation between A and B. This makes our problem more challenging from both computational and memory consumption perspectives.

Correlated subgraphs mining in graph databases. The closest related work in the space of correlated subgraphs mining is by Ke et al. [14]. However, there are two fundamental differences:

(1) Definition of correlation: Ke et al. target the graph database scenario where there are multiple graphs: two subgraphs A and B are called correlated if the containment of A within a data graph increases the likelihood of containing B as well. In our problem, we have only one large data graph. In this graph, subgraphs A and B are defined to be correlated if the instances of A are frequently located in close proximity to the instances of B.

(2) Notion of proximity: Owing to the difference in the definition of correlation, there is no concept of proximity in [14]. In our problem, for each instance of a subgraph, we need to search and track instances of all other subgraphs that occur within a user-specified distance threshold. This operation is the root of the primary computational bottleneck, which does not arise in [14].

Relaxed notions of frequent subgraphs mining. Our problem also has similarities with various relaxed definitions for frequent subgraphs mining and search. For example, proximity patterns [15] were introduced to mine the top-k set of node labels that co-occur frequently in neighbourhoods. Correlations between node labels and dense graph structures were identified in [16, 17]. In our problem, while we allow certain flexibility in terms of how the constituent subgraph instances are connected, we still maintain fixed structures for subgraph instances.

[Our Algorithmic Contributions] In spite of the aforementioned challenges and fundamental differences with existing literature, it is still desirable to obtain CSM results within minutes over real networks containing millions of nodes. In this work, we achieve this task with our novel algorithmic contributions.

In particular, the key differentiating factor in our problem compared to existing subgraphs mining problems is that we not only need to identify the subgraph patterns, but also enumerate and store all its instances. This requirement imposes a huge scalability challenge on both computation and storage. We address this issue by designing a novel data structure called “Replica”, which stores all instances of a subgraph pattern on-demand in a compressed manner. Using Replica as the data storage platform, we design a single-step, best-first exploration algorithm to detect correlated subgraph pairs efficiently. We also discuss the novelty of the Replica over existing compressed structures for various graph mining tasks, as well as its potential applicability in other workloads. We further speed up the mining process by designing a near-optimal approximation algorithm.

For more information, click here for our paper. Code: GitHub.

[Reference]
[1] X. Yan and J. Han. “gSpan: Graph-Based Substructure Pattern Mining”. In ICDM, 2002.
[2] M. Worlein, T. Meinl, I. Fischer, and M. Philippsen. “A Quantitative Comparison of the Subgraph Miners MoFa, gSpan, FFSM, and Gaston”. In PKDD, 2005.
[3] X. Yan, H. Cheng, J. Han, and P. S. Yu. “Mining Significant Graph Patterns by Leap Search”. In SIGMOD, 2008.
[4] S. Ranu, M. Hoang, and A. Singh. “Mining Discriminative Subgraphs from Global-state Networks”. In KDD, 2013.
[5] M. A. Hasan and M. J. Zaki. “Output Space Sampling for Graph Patterns”. PVLDB, 2(1):730–741, 2009.
[6] S. Ranu and A. Singh. “GraphSig: A Scalable Approach to Mining Significant Subgraphs in Large Graph Databases”. In ICDE, 2009.
[7] S. Ranu, B. T. Calhoun, A. K. Singh, and S. J. Swamidass. “Probabilistic Substructure Mining From Small-Molecule Screens”. Molecular Informatics, 30(9):809–815, 2011.
[8] S. Ranu and A. K. Singh. Mining Statistically Significant Molecular Substructures for Efficient Molecular Classification. Journal of Chemical Information and Modeling, 49:2537–2550, 2009.
[9] S. Ranu and A. K. Singh. Indexing and Mining Topological Patterns for Drug Discovery. In EDBT, 2012.
[10] M. A. Hasan, V. Chaoji, S. Salem, J. Besson, and M. J. Zaki. “ORIGAMI: Mining Representative Orthogonal Graph Patterns”. In ICDM, 2007.
[11] S. Zhang, J. Yang, and S. Li. “RING: An Integrated Method for Frequent Representative Subgraph Mining”. In ICDM, 2009.
[12] D. Natarajan and S. Ranu. “A Scalable and Generic Framework to Mine Top-k Representative Subgraph Patterns”. In ICDM, 2016.
[13] S. Ranu, M. Hoang, and A. Singh. “Answering Top-k Representative Queries on Graph Databases”. In SIGMOD, 2014.
[14] Y. Ke, J. Cheng, and J. X. Yu. “Efficient Discovery of Frequent Correlated Subgraph Pairs”. In ICDM, 2009.
[15] A. Khan, X. Yan, and K.-L. Wu. “Towards Proximity Pattern Mining in Large Graphs”. In SIGMOD, 2010.
[16] Z. Guan, J. Wu, Q. Zhang, A. Singh, and X. Yan. “Assessing and Ranking Structural Correlations in Graphs”. In SIGMOD, 2011.
[17] A. Silva, J. W. Meira, and M. J. Zaki. “Mining Attribute-structure Correlated Patterns in Large Attributed Graphs”. PVLDB, 5(5):466–477, 2012.
[18] E. A. Lee, S. Fung, H. Sze-To, and A. K. C. Wong. “Discovering Co-occurring Patterns and their Biological Significance in Protein Families”. BMC Bioinformatics, 15(S-12):S2, 2014.
[19] Source for Yeast dataset. http://string-db.org/cgi/download.pl.
[20] Source for LastFM dataset. https://www.last.fm/.
[21] Source for Coauthor and Citation (DBLP) datasets. https://www.aminer.org/citation.
[22] GO for utility process. http://www.candidagenome.org/cgi-bin/GO/go.pl?goid=1901522.
[23] R. Koike, T. Amemiya, M. Ota, and A. Kidera. “Protein Structural Change upon Ligand Binding Correlates with Enzymatic Reaction Mechanism”. Journal of molecular biology, 379:397–401, 07 2008.
[24] R. Koike, A. Kidera, and M. Ota. “Alteration of State and Domain Architecture is Essential for Functional Transformation between Transferase and Hydrolase with the Same Scaffold”. Protein Science: a Publication of the Protein Society, 18:2060–6, 10 2009.

Sunday, April 19, 2020

Reliability Maximization in Uncertain Graphs

Reliability Maximization in Uncertain Graphs


A summary of the IEEE TKDE 2020 research paper by Xiangyu Ke, Arijit Khan, Mohammad Al Hasan, and Rojin Rezvansangsari

[Background]  Rich expressiveness of probabilistic graphs and their utility to model the inherent uncertainty in a wide range of applications have prompted a large number of research works on probabilistic graphs by the data management research communities [1]. In an uncertain graph setting, Network Reliability is a well-studied problem [2], [3], which requires to measure the probability that a target node is reachable from a source node. Reliability has been widely studied in device networks, i.e., networks whose nodes are electronic devices and the (physical) links between such devices have a probability of failure [4]. More recently, the attention has been shifted to social, communication, transportation, genomic, and logistic networks [5]–[7]. 

Figure 1: Reliability in a sensor network: the probabilities of successful package delivery rate from a sensor to another.

[Our Problem] Given an uncertain graph, a source node s, a target node t, a probability threshold ζ ∈ (0, 1], and a small positive integer k, we investigate to find the top-k edges to add in the graph, each with probability ζ, so that the reliability from the source s to the target t is maximized.

[Application Scenarios] (1) In mobile ad-hoc networks, the connectivity between sensor nodes and devices is estimated using noisy measurements, thus leading to edges naturally associated with a probability of existence [7]. Road networks can be modeled as uncertain graphs because of unexpected traffic congestion [6]. In these networks, creating new connections between nodes (e.g., building new roads, flyovers, adding Ethernet cables) is limited by physical constraints and budget. One can introduce only k new edges where k is decided based on resource constraints. (2) In social networks, finding k best shortcut edges could maximize the information diffusion probability from an early adopter to a target customer [8], thus the network host can actively recommend these links to the respective users. (3) In case of protein-interaction networks, interactions are established for a limited number of proteins through noisy and error-prone experiments—each edge is associated with a probability accounting for the existence of the interaction. Therefore, finding the top-k shortcut edges can assist in de-noising protein-interaction networks [9].

[Challenges and Our Theoretical Contributions] (1) The computation of s-t reliability is #P-hard [2][3]. Even if polynomial time reliability estimation methods are employed, we prove the following. (2) Our problem is NP-hard, and does not admit any PTAS. (3) The underlying objective function is neither submodular, nor supermodular. (4) The optimal solution changes if input probabilities on new edges vary. (5) The optimal solution changes if the probabilities in the  input graph vary. (6) The optimal solution for budget (#new edges) k is not a subset of that for budget r when k<r. (7) If the direct edge from s to t, st, is missing in the input graph, and is allowed to be added, st will always be included in the top-k optimal solution.

[Algorithmic Contributions] In spite of such challenges, we devise efficient algorithms. (1) We investigate several baselines, analyse their complexities, and discuss the shortcomings. They include individual top-k edge selection, hill-climbing method, centrality-based method, and eigenvalue-based method. (2) We eliminate the search space (can be up to O(n^2) in sparse real networks) via finding the promising nodes with high original reliability from the source, or to the target. (3) After adding all possible missing edges only between pairs of promising nodes, we further filter out those paths with low probabilities from s to t. The intuition is that what really matters in computing the reliability between two nodes is the set of highly reliable paths between them [10]-[12]. (4) We adapt the single-path-inclusion algorithm in [10] to our problem setting, and refine it in a path-batch manner to significantly improve the accuracy. 

[Other Queries] We also consider a restricted and one extended version of our problem to support a wider family of queries. (1) In the restricted version, the reliability is estimated only by the most reliable path, thus it can be solved in polynomial-time. (2) In the extended version, multiple sources and targets can be provided as input. We investigate several possible reliability aggregation functions. The proposed algorithms are generalized to each case.

[Case Study] The Intel Lab Data (http://db.csail.mit.edu/labdata/labdata.html) dataset contains the sensor network information with 54 sensors deployed in the Intel Berkeley Research Lab (map given in Figures 2 and 3). The probabilities on links denote the percentages of messages from a sender successfully reached to a receiver. Only those links with probabilities higher than the average value (0.33) are shown in the figures, and the thickness represents link probabilities. Due to budget constraints, only 3 new links are allowed for each case. We further assume that the probability of each new link would be the same as the average edge probability of the original dataset, that is, 0.33. We notice that if two sensors are more than 20 meters away, the original link probability between them is usually close to 0. Thus, we only allow establishing new links between a pair of sensors that are at most 15 meters away.


Figure 2: Improving the reliability from sensor 21 (right) to 46 (left) with 3 new links (marked by dotted lines). 
The original reliability is 0.4, and the resultant reliability is 0.88.

Figure 3: Improving the reliability from sensor 15 to 40 (on the diagonal) with 3 new links (marked by dotted lines). 
The original reliability is 0.28, and the resultant reliability is 0.58.

    For case (1), sensor 46 has very weak connections from outside, while sensor 21 is connected with the bottom part of the lab, where a very dense network exists. Therefore, our solution for this case is to connect sensor 46 with sensors in the bottom part of the lab. By establishing three links 2 to 46, 35 to 46, and 37 to 46, we improve the reliability between 21 to 46 from 0.40 to 0.88.

    For case (2), notice in Figure 7 that the sensors in the center part of lab are well-connected, and the links in this region are thicker than those in the bottom part. The source sensor 15 has a few connections with sensors in the bottom part, but no link with those in the center part. The destination sensor 40 has limited connections beyond its physical neighbors. Existing configuration offers a poor reliability of 0.28 for the connection between source and destination which we like to improve. The smart decision made by our algorithm is as follows: First, connect sensor 35 to 40, thus making sensor 35 a bridge between the center and the bottom region of the network; Second, enable connection from sensor 15 to the center part (by establishing link from 15 to 10, and from 15 to 11). This results in 0.58 overall reliability from sensor 15 to 40, which is more than double of the original reliability value. 

    These results illustrate how our proposed solution for the budgeted reliability maximization problem can be useful in solving real-life problems.

For more information, click here for our paper. 
Blog post contributed by: Xiangyu Ke


[Reference]

[1] A. Khan, Y. Ye, and L. Chen, “On Uncertain Graphs”, Morgan & Claypool Publishers, Synthesis Lectures on Data Management, 2018.

[2] M. O. Ball, “Computational Complexity of Network Reliability Analysis: An Overview”, IEEE Tran. Rel., vol. 35, no. 3, pp. 230–239, 1986.

[3] L. G. Valiant, “The Complexity of Enumeration and Reliability Problems”, SIAM J. on Computing, vol. 8, no. 3, pp. 410–421, 1979.

[4] K. K. Aggarwal, K. B. Misra, and J. S. Gupta, “Reliability Evaluation: A Comparative Study of Different Techniques” Micro. Rel., vol. 14, no. 1, 1975.

[5] D. Kempe, J. M. Kleinberg, and E. Tardos, “Maximizing the Spread of Influence through a Social Network”, in KDD, 2003.

[6] M. Hua and J. Pei, “Probabilistic Path Queries in Road Networks: Traffic Uncertainty aware Path Selection”, in EDBT, 2010.

[7] J. Ghosh, H. Q. Ngo, S. Yoon, and C. Qiao, “On a Routing Problem Within Probabilistic Graphs and its Application to Intermittently Connected Networks”, in INFOCOM, 2007.

[8] C. Chen, H. Tong, B. A. Prakash, T. Eliassi-Rad, M. Faloutsos, and C. Faloutsos, “Eigen-Optimization on Large Graphs by Edge Manipulation”, ACM Trans. Knowl. Discov. Data, vol. 10, no. 4, pp. 49:1–49:30, 2016.

[9] O. Kuchaiev, M. Rasajski, D. J. Higham, and N. Przulj, “Geometric De-noising of Protein-Protein Interaction Networks”, PLOS Computational Biology, vol. 5, no. 8, pp. 1–10, 08 2009.

[10] A. Khan, F. Bonchi, F. Gullo, and A. Nufer, “Conditional Reliability in Uncertain Graphs”, IEEE Trans. Knowl. Data Eng., vol. 30, no. 1, pp. 2078–2092, 2018.

[11] W. Chen, C.Wang, and Y.Wang, “Scalable Influence Maximization for Prevalent Viral Marketing in Large-Scale Social Networks”, in KDD, 2010.

[12] A. Khan, B. Zehnder, and D. Kossmann, “Revenue Maximization by Viral Marketing: A Social Network Host’s Perspective”, in ICDE, 2016.

Tuesday, March 17, 2020

Semantic Guided and Response Times Bounded Top-k Similarity Search over Knowledge Graphs

Semantic Guided and Response Times Bounded Top-k Similarity Search over Knowledge Graphs

A summary of the IEEE ICDE 2020 research paper by Yuxiang Wang, Arijit Khan, Tianxing Wu, Jiahui Jin, and Haijiang Yan.

Background: Knowledge graphs (such as DBpedia [1], Yago [2], and Freebase [3]) have been constructed in recent years, managing large-scale and real-world facts as a graph [4]. In such graphs, each node represents an entity with attributes, and each edge denotes a relationship between two entities. 

Answering Graph Query on Knowledge Graphs: Querying knowledge graphs is essential for a wide range of applications, e.g., question answering and semantic search [5]. For example, consider that a user wants to find all cars produced in Germany. One can come up with a reasonable graph representation of this query as a query graph GQ, and identify the exact or approximate matches of GQ in a knowledge graph G using graph query models [6]–[10]. Correct answers can be returned, such as <BMW 320, assembly, Germany>. Graph query also acts as a fundamental component for other query forms, such as keyword and natural language query [9]. We can reduce these query forms to a graph query by translating input text to a query graph [11], [12].

To retrieve the information of interest from a knowledge graph G, users are often required to have full knowledge of the vocabulary used in G [13], as well as the underlying schemas defined in G, which is difficult for ordinary users (even professional users) [14]. Otherwise, the user-built query graph is likely to be structurally different from the predefined schemas, thus fails to return correct answers due to the mismatch with the query graph. Consider the following motivating example.

Consider the query: Find all cars that are produced in Germany (Q117 from QALD-4 benchmark [15]). Figure 1 provides four correct graph matches with different schemas in DBpedia. Each one is represented as an n-hop path. An ordinary user may build a query graph G1Q based on the phrases from the natural language question [12]. While a professional user may build G2Q by using the controlled vocabulary (e.g., Automobile is used to represent vehicles in DBpedia) and a schema she already knew. However, both query graphs suffer from the structural mismatch problem.

Fig. 1: An example of structural mismatch with query graphs: different users may employ different query graphs (top) to find all cars made in Germany. Four correct graph matches in DBpedia are provided (bottom). Only G2Q can retrieve partial correct answers having the same schemas as 1 , because the 1-hop edge assembly cannot match any n-hop (n > 1) paths.

Challenges: 

Mismatch in query nodes. In G1Q, a query node with type Car represents the phrase “cars”. However, no entity in DBpedia has the same, or even a textually similar type for Car, because it is not a term belonging to the controlled vocabulary of DBpedia. Hence, G1Q fails to find correct answers.

Mismatch in query edges. For G2Q, the user can retrieve 234 answers that have the same schema as graph match 1. However, more than 200 correct answers are ignored, because a 1-hop edge in G2Q cannot be mapped to the semantically similar n-hop (n > 1) paths (edge-to-path mapping).

If a user has full knowledge about DBpedia, then she can build various query graphs that cover all possible schemas, to obtain all cars of interest. Generally, it is a strong assumption. As an alternative, we aim to provide a graph query system that will be able to support different query graphs without forcing users to use very controlled vocabulary or be knowledgeable about the dataset. This motivates us to fill the structural gap in graph matching by considering the semantics of query graphs. 

Our Solution for Semantic-Guided Search: In this work, we develop a semantic-guided search to find the semantically similar paths to query edges without prior knowledge. To the best of our knowledge, we are the first to support semantically edge-to-path mapping in graph query. Moreover, we handle  query node mismatch via a node transformation library. Figure 2 shows the pipeline of our approach, which has an offline and an online phase.

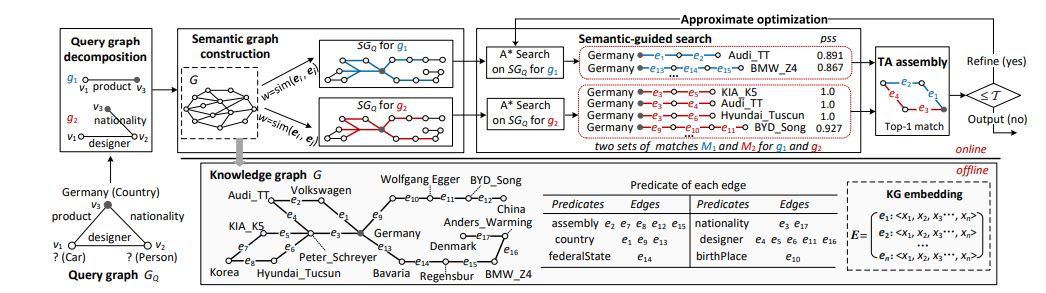
Fig. 2: A running example of our approach, including offline KG embedding (bottom right) and online query processing. Four components of the online part are: (1) Query graph decomposition, (2) Semantic graph construction, (3) Semantic-guided search, and (4) Threshold Algorithm-based assembly. An approximate optimization is applied for response-time-bounded query. All predicates in the example knowledge graph are provided in a table (bottom middle).

Offline phase. Given a knowledge graph G, we leverage a knowledge graph embedding model [4], [18] to represent the predicates of G in a vector space E. Hence, the semantic similarities of predicates can be easily obtained through vector calculation, and this makes it possible to achieve the semantic similarities of a path in G to a query edge in GQ. To be precise, this is essential for semantically edge-to-path mapping.

Online phase. In Figure 2, we take a query graph GQ as an input. We adopt a decomposition-assembly framework for GQ, which consists of four basic components.

(1) Query graph decomposition. We first decompose GQ into a set of sub-query graphs {g1...gn} by a dynamic programming algorithm, subject to minimizing the possible query cost. 

(2) Semantic graph construction. To support the semantically edge-to-path mapping, we then construct a semantic graph SGQ for each sub-query graph gi by preserving the predicate semantic similarities on the edges of G. In Figure 2, we show example semantic graphs for g1 and g2. For instance, each blue edge has a high semantic similarity to the query edge product, e.g., e2 (assembly) has 0.98 semantic similarity to product. By utilizing these similarities in SGQ, we define the path semantic similarity (pss) to measure how semantically similar a path in G is to gi.

(3) Semantic-guided search. We next present an A* semantic search to find the top-k semantically similar matches for each sub-query graph gi from the semantic graph SGQ based on the path semantic similarity (pss). To improve the efficiency, we propose a well-designed heuristic estimation function of pss that prunes the search space. We prove the effectiveness guarantee of our A* semantic search, that is, the matches with the greatest pss must be found.

(4) Threshold Algorithm (TA)-based assembly. Finally, we assemble the matches of all sub-query graphs based on the threshold algorithm (TA) [17], in order to form the final answers for GQ.

Response-Time Bounded Search: Another crucial problem involves improving the system response time (SRT) for a graph query. SRT is the amount of time that a user waits before viewing results [16]. A shorter SRT usually indicates a better user experience. To the best of our knowledge, no current state-of-the-art work supports response-time-bounded graph query. In this work, we present an approximate optimization on our semantic-guided search to enable a trade-off between accuracy and the system response time (SRT) within a user-specified time bound T. As more time is given, more high-quality matches are refined incrementally. We prove that the globally optimal matches for GQ can be achieved theoretically when sufficient time is given.

In summary, we blend semantic-guided and response-time bounded characteristics in one system to support the top-k graph query over a knowledge graph effectively and efficiently. We have evaluated the effectiveness and efficiency of our approach through extensive experiments on three real-world and large-scale knowledge graphs.

For more information, click here for our paper.  Codes and Datasets: GitHub.
Blog post contributed by: Arijit Khan
  
[Reference]

[1] P. N. Mendes, M. Jakob, and C. Bizer, “Dbpedia: A multilingual crossdomain knowledge base.” in LREC, 2012, pp. 1813–1817. 

[2] J. Hoffart, F. M. Suchanek, K. Berberich, and G. Weikum, “Yago2: A spatially and temporally enhanced knowledge base from wikipedia,” Artificial Intelligence, vol. 194, pp. 28–61, 2013. 

[3] K. Bollacker, R. Cook, and P. Tufts, “Freebase: A shared database of structured general human knowledge,” in AAAI, 2007, pp. 1962–1963. 

[4] X. Huang, J. Zhang, D. Li, and P. Li, “Knowledge graph embedding based question answering,” in WSDM, 2019, pp. 105–113. 

[5] R. V. Guha, R. McCool, and E. Miller, “Semantic search,” in WWW, 2003, pp. 700–709. 

[6] A. Khan, Y. Wu, C. C. Aggarwal, and X. Yan, “Nema: Fast graph search with label similarity,” PVLDB, vol. 6, no. 3, pp. 181–192, 2013. 

[7] L. Zou, R. Huang, H. Wang, J. X. Yu, W. He, and D. Zhao, “Natural language question answering over rdf: a graph data driven approach,” in SIGMOD, 2014, pp. 313–324. 

[8] S. Yang, Y. Wu, H. Sun, and X. Yan, “Schemaless and structureless graph querying,” PVLDB, vol. 7, no. 7, pp. 565–576, 2014. 

[9] S. Yang, F. Han, Y. Wu, and X. Yan, “Fast top-k search in knowledge graphs,” in ICDE, 2016, pp. 990–1001. 

[10] J. Jin, S. Khemarat, and L. Gao, “Querying web scale information networks via bounding matching scores,” in WWW, 2015, pp. 527–537. 

[11] W. Zheng, L. Zou, X. Lian, J. X. Yu, S. Song, and D. Zhao, “How to build templates for rdf question/answering: An uncertain graph similarity join approach,” in SIGMOD, 2015, pp. 1809–1824. 

[12] S. Han, L. Zou, J. X. Yu, and D. Zhao, “Keyword search on rdf graphs-a query graph assembly approach,” in CIKM, 2017, pp. 227–236. 

[13] S. Shekarpour, E. Marx, S. Auer, and A. Sheth, “Rquery: rewriting natural language queries on knowledge graphs to alleviate the vocabulary mismatch problem,” in AAAI, 2017, pp. 3936–3943.

[14] W. Zheng, L. Zou, W. Peng, X. Yan, S. Song, and D. Zhao, “Semantic sparql similarity search over rdf knowledge graphs,” PVLDB, vol. 9, no. 11, pp. 840–851, 2016. 

[15] “Qald-4,” http://qald.aksw.org/index.php?x=challenge&q=4. 

[16] S. S. Bhowmick, B. Choi, and S. Zhou, “Vogue: Towards a visual interaction-aware graph query processing framework,” in CIDR, 2013.

[17] R. Fagin, A. Lotem, and M. Naor, “Optimal aggregation algorithms for middleware,” in PODS, 2001.

[18] A. Bordes, N. Usunier, A. Garc´ıa-Duran, J. Weston, and O. Yakhnenko, “Translating embeddings for modeling multi-relational data,” in NIPS, 2013, pp. 2787–2795.
Subscribe to: Posts (Atom)